Tables

Class DS_TABLE

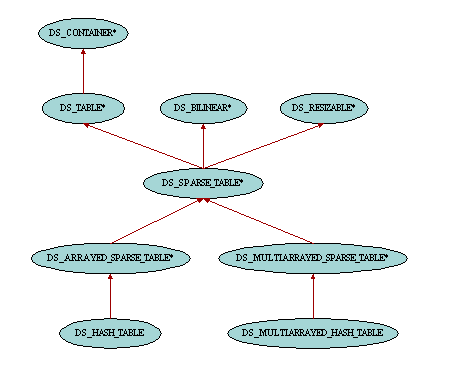
Tables are data structures whose items are accessible by keys. Therefore the class DS_TABLE has two generic parameters. As for all other container classes, the first parameter G represents the type of the items, whereas the second parameter K is the type of the keys which are associated with the items. The features provided by class DS_TABLE are very similar to some of those of class DS_INDEXABLE. The difference comes from the fact that in DS_INDEXABLE keys are contiguous integers whereas in DS_TABLE keys can be of any type, and hence not necessarily contiguous. The main features introduced in class DS_TABLE are item to access items by key, put to insert new items and replace to associate an existing key with another item, remove to remove an item and its associated key from the table, valid_key to check whether a key can be used in the table and has to check whether an item has already been inserted in the table with a given key.

Class DS_HASH_TABLE

One possible implementation of tables is hash tables. A hash table is typically made up of an array where items are accessed by integer index. Therefore the keys used in the hash tables should provide a means to yield such integer value through a hashing mechanism. This is exactly what feature hash_code from HASHABLE is for, and therefore the second generic parameter of DS_HASH_TABLE is constrained by HASHABLE. Thanks to this implementation, features of hash tables are usually more efficient than linked implementations since access time in an array is bounded by a constant regardless of the number of items in the container. However the hash code associated with the keys is not necessarily unique, and therefore collisions may happen and hence slow down the process. The efficiency of hash tables hence depends on the number of collisions that may occur in the table. Therefore the implementation for the hash_code of the keys is very important since returning often the same value for different keys will trigger too many collisions and yield performance degradations. If the default implementation of hash_code is not optimal for a given set of keys, one can inherit from DS_HASH_TABLE and redefine its feature hash_position to provide a better implementation. For example, consider a school which keeps track of project assignments in a table indexed by students. The obvious solution is to declare:

assignments: DS_HASH_TABLE [PROJECT, STUDENT]

However the implementation of hash_code in class STUDENT inherited from PERSON just returns the age of the person. This implementation of hash_code in class PERSON is perfectly valid in most cases, but it is clear that when dealing with students in the same classroom it is likely that they will all have more or less the same age and hence the same hash code. In this particular case it is better to provide a better implementation for hash_position in DS_HASH_TABLE to avoid the numerous collisions:

class ASSIGNMENTS
inherit
    DS_HASH_TABLE [PROJECT, STUDENT]
        redefine
            hash_position
        end
create
    make
feature {NONE} -- Implementation
    hash_position (s: STUDENT): INTEGER is
            -- Hash position of student s in internal array
        do
            if s /= Void then
                Result := s.name.hash_code \\ modulus
            else
                Result := modulus
            end
        end
end 

The keys are directly stored in the hash table without being copied. Therefore it is important that the hash code associated with each key doesn't change while the key is stored in the hash table. Otherwise the hashing mechanism would be broken and it would be impossible to access the item associated with this key. Likewise, keys are compared in the hash table using the feature key_equality_tester of type DS_EQUALITY_TESTER. Therefore if the critera used to implement the function test in DS_EQUALITY_TESTER are changed while the key is stored in the hash table, this key might not be recognized properly anymore within this hash table. Needless to say that if two keys are considered equal, they should have the same hash code. The solution when the hash code or equality criteria of a key are likely to vary while the key is stored in the hash table is to clone that key when inserting an item associated with it.

The class DS_HASH_TABLE provides traversal facilities inherited from DS_BILINEAR. Although all items will be visited once and only once during a traversal, they will be traversed in an unpredictable order and subsequent traversals may traverse the items in different orders. This is because a hash table is not an ordered container as can a list be. Items are not inserted before or after other items in the hash table but based on a hashing mechanism and collision-resolution algorithm. The only way to get a guaranteed ordered hash table with the current implementation is to use exclusively feature force_last to insert items.

As you may now realize after reading the first paragraph above, the performance of hash tables is one of their raison d'être. This had of course to be taken into account when implementing the routines inherited from DS_TABLE. Because of the precondition of item which states that in order to be able to query an item associated with a given key, that item has to exist in the first place, one has to write:

if table.has (k) then
    v := table.item (k)
else
    ...
end

However, both has and item will have to compute the hash code of k and deal with possible collisions in the hash table. In other words we do twice the same thing. The solution adopted in the current implementation of DS_HASH_TABLE is to keep track of the result of the last hashing operation in the hash table in a cache. Therefore, in the code above, most of the work of accessing the item at key k will be done only once in the routine has, and item will realize that the key given as argument is the same and hence avoid calling the hashing mechanism again.

Another solution to avoid that would have been to get rid of the precondition in item and return Void when there is no item associated with key k. However this solution goes against the principle of Design by Contract since getting Void could either mean that there is no item for key k or that there is actually one which happens to be Void. Therefore this solution has not been adopted in DS_HASH_TABLE but a better designed alternative also based on the try-and-see principle is available:

table.search (k)
if table.found then
    v := table.found_item
else
    ...
end

Both code excerpts should have the same execution time performance thanks to DS_HASH_TABLE's internal optimizations. Using one or the other is just a question of taste.

Class DS_MULTIARRAYED_HASH_TABLE

When hash tables contain a very large number of items, the implementation of DS_HASH_TABLE may reach some limits since the internal arrays become too huge and resizing them may yield memory problems. The class DS_MULTIARRAYED_HASH_TABLE provides the same functionalities as DS_HASH_TABLE but uses a sequence of fixed size arrays instead of a single array for its implementation. These array chunks are only created when first accessed and resizing the whole table does only require to add one or several chunks to the sequence and therefore avoids having to resize big arrays.

Copyright © 2000-2016, Eric Bezault mailto:ericb@gobosoft.com http://www.gobosoft.com Last Updated: 26 December 2016