| Sets |
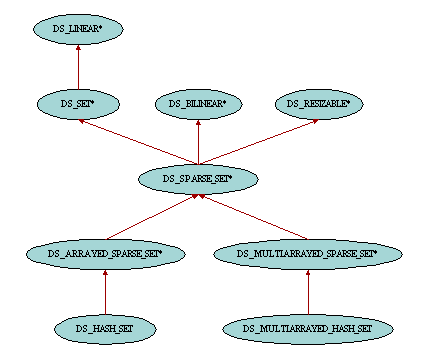
Sets are data structures whose items appear only once. Therefore occurrences has either value 1 or 0 depending on the fact that the object is included in the set or not. The main property of sets is that they can be compared using boolean queries: is_subset to know whether all items of one set are included in another set, is_superset to know whether one set contains all items of another set, and is_disjoint to find out whether two sets have no item in common. The class DS_SET has also four basic operations: append to get the union of two sets, intersect removes the items which are not in the second set, subtract removes the items which are also included in the second set, and symdif to get the symmetric difference.
One possible implementation of sets is hash sets. A hash set is typically made up of an array where items are accessed by integer index. Therefore the items used in the hash sets should provide a means to yield such integer value through a hashing mechanism. This is exactly what feature hash_code from HASHABLE is for, and therefore the generic parameter of DS_HASH_SET is constrained by HASHABLE. Thanks to this implementation, features of hash sets are usually more efficient than linked implementations since access time in an array is bounded by a constant regardless of the number of items in the container. However the hash code associated with the items is not necessarily unique, and therefore collisions may happen and hence slow down the process. Therefore, as for hash tables, the efficiency of hash sets depends on the number of collisions that may occur in the set. Please have a look at the chapter about hash tables for further discussions about hash codes, collisions and how to avoid performance degradations.
The class DS_HASH_SET provides traversal facilities inherited from DS_BILINEAR. Although all items will be visited once and only once during a traversal, they will be traversed in an unpredictable order and subsequent traversals may traverse the items in different orders. This is because a hash set is not an ordered container as can a list be. Items are not inserted before or after other items in the hash set but based on a hashing mechanism and collision-resolution algorithm. The only way to get a guaranteed ordered hash set with the current implementation is to use exclusively feature force_last to insert items.
When hash sets contain a very large number of items, the implementation of DS_HASH_SET may reach some limits since the internal arrays become too huge and resizing them may yield memory problems. The class DS_MULTIARRAYED_HASH_SET provides the same functionalities as DS_HASH_SET but uses a sequence of fixed size arrays instead of a single array for its implementation. These array chunks are only created when first accessed and resizing the whole set does only require to add one or several chunks to the sequence and therefore avoids having to resize big arrays.
|
Copyright © 2001-2016, Eric
Bezault mailto:ericb@gobosoft.com http://www.gobosoft.com Last Updated: 26 December 2016 |