| Lists |
A list is an ordered sequence of items. This doesn't necessarily mean that the items are sorted but rather that the container can be traversed in a predictable way. Thanks to multiple inheritance, DS_LIST is equipped with several basic facilities: lists can be traversed forward and backward, they can be sorted, they can be searched and their items can also be accessed by index.
Items can be added to or removed from the list relative to their index position thanks to the features inherited from DS_INDEXABLE. Examples of such features are put and force to add one item at a time, extend and append to add several items at once, remove to remove one item and prune to remove several items. For convenience, these routines also have two counterparts which deal with the first item of the list (at index 1) and the last item of the list (at index count). For instance, in order to add an item v at the beginning of the list, one can just call put_first (v) which is just a synomym of put (v, 1).
But DS_LIST also introduces other features to add and remove items relative to a cursor position. Considering that the first item of the list is graphically located to the left, the last item to the right, and other items ordered in-between, one can add items to the left or to the right of a given cursor and remove items to the left, to the right or at the cursor position. For example, in order to add an item v to the right of cursor position in list, one can just call list.put_right_cursor (v, cursor). Alternatively one can call cursor.put_right (v). Because of the design decision which was taken to have both internal and external cursors, similar routines acting relatively to the internal cursor position of the list are available as well. These routines have the same names as their external cursor counterparts except that they don't have the suffix _cursor. Therefore list.put_right (v) will add an item v to the right of current internal cursor position of the list.
Class DS_LIST and its associated cursor class DS_LIST_CURSOR have many other features which have not been described here. Please have a look at their flat-short forms for details.
The Gobo Eiffel Structure Library provides three implementations for list containers: DS_LINKED_LIST implemented with singly linkable cells, DS_BILINKED_LIST with doubly linkable cells and DS_ARRAYED_LIST implemented with an array. The reason for having all these different implementations is that they have different memory space or time performance. But one is not better that the others, it just depends on the kind of operations to be applied to the list and on the memory/time tradeoff one is ready to accept. In order to help you choose the most appropriate list implementation for a particular use, the information about the complexity of the operations has been added to the header comment of almost all of the access, insertion and removal routines. For example, in the header comment of feature put_first in class DS_ARRAYED_LIST one can read -- (Performance: O(count).). This means that the execution time is on average proportional to the number of items in the list. On the other hand the header comment of put_first in class DS_LINKED_LIST says -- (Performance: O(1).). This means that the execution time is bounded by a constant. But this doesn't mean that class DS_LINKED_LIST has a better implementation than DS_ARRAYED_LIST. For example routine go_i_th will perform better with DS_ARRAYED_LIST.
A list of type DS_LINKED_LIST is made up of individual linkable cells, instances of class DS_LINKABLE, each of these cells containing an item of the list and being linked to the cell containing the next item. Following is a simplified graphical representation of the memory layout of a linked list.
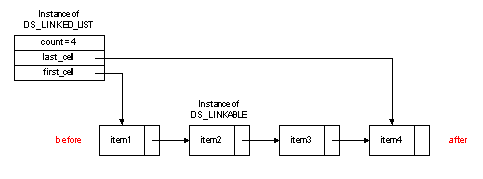
After a quick look at this picture, it is easy to understand that traversing the list from left to right will be quite efficient since each cell has a reference to its right neighbor. However, backward traversals will be expensive since the cells will have to be visited from the first cell to the cell on the left of the current position each time back is called. Likewise, insertions and deletions to the right of a cursor position will be cheap whereas they will be expensive if they happen to the left of the cursor. And finally, thanks to the reference to the last cell of the list, insertions to the end of the list do not require the full list to be traversed, making a good tradeoff between memory space and execution time.
The inefficiencies that we pointed out in the linked implementation of lists can be easily addressed just by using linkable cells which not only have a reference to their right neighbor but also keep a reference to their left neighbor. Class DS_BILINKED_LIST provides such an implementation since it uses DS_BILINKABLE cells.
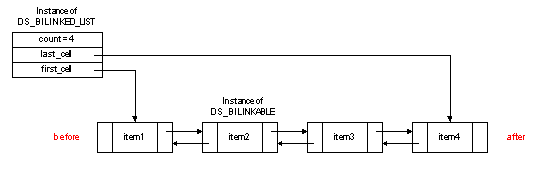
As always, what we gained in execution time improvement, we lost it in memory occupation as we can see on the above picture. Therefore, when you need a list which requires to call more than occasionally features such as back and the like, you are better off using DS_BILINKED_LIST. Otherwise, there is no need to waste memory space when DS_LINKED_LIST would just do the job as efficiently.
One thing that DS_LINKED_LIST and DS_BILINKED_LIST are not good at is accessing and modifying the list based on the index values. This is simply because these operations would require to traverse the cells one by one until as many cells as the given index have been visited. Class DS_ARRAYED_LIST provides an implementation based on ARRAY, and therefore addresses this problem.
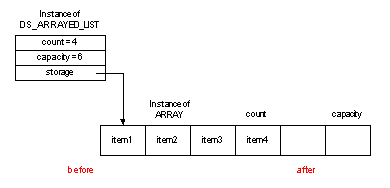
On the other hand, the class DS_ARRAYED_LIST is not very good at inserting or removing items unless they are at the end of the list. This is because the items to the right of the altered position have to be moved either to the right (insertion) or to the left (removal). Also, to avoid too many resizings of the array when inserting items to the list, the allocated space is often larger than the number of items actually held in the list. Therefore you should use DS_ARRAYED_LIST if most of your insertion and removal operations are applied to the end of the list, if you know in advance the number of items that will be held in the list to avoid wasting time resizing the underlying array, and if you often access items by index. Otherwise, and in particular if items are most of the time inserted in or removed from the middle or beginning of the list, singly and doubly linked implementation of list is propably what you need.
|
Copyright © 1999-2016, Eric
Bezault mailto:ericb@gobosoft.com http://www.gobosoft.com Last Updated: 26 December 2016 |